Seed Prover 1.5: Advanced Mathematical Reasoning through a Novel Agentic Architecture
This July, the ByteDance Seed team participated in the International Mathematical Olympiad (IMO) 2025 by invitation. Over three days of attempts, our formal mathematical reasoning model, Seed Prover, fully solved four of the six problems and partially proved another, achieving an officially recognized silver-medal performance.
Recently, we have rolled out Seed Prover 1.5, a new-generation specialized model for formal mathematical reasoning. Through large-scale Agentic Reinforcement Learning (RL) training, its reasoning capability and efficiency have advanced significantly. Compared to its predecessor, Seed Prover 1.5 generated complete, compilable, and verifiable Lean proof code for the first five IMO 2025 problems within 16.5 hours. This corresponds to a score of 35/42, reaching the gold-medal cutoff under previous IMO scoring standards.
In the undergraduate-level North American mathematics competition, the Putnam, Seed Prover 1.5 produced compilable and verifiable Lean proof code for 11 of the 12 problems from Putnam 2025 within 9 hours. In more systematic evaluations, the model delivered outstanding results: It solved 88% of problems in the full PutnamBench (undergraduate level), 80% in Fate-H (graduate level), and 33% in Fate-X (PhD level). This establishes a new state-of-the-art (SOTA) for formal mathematical reasoning models across these benchmark datasets.
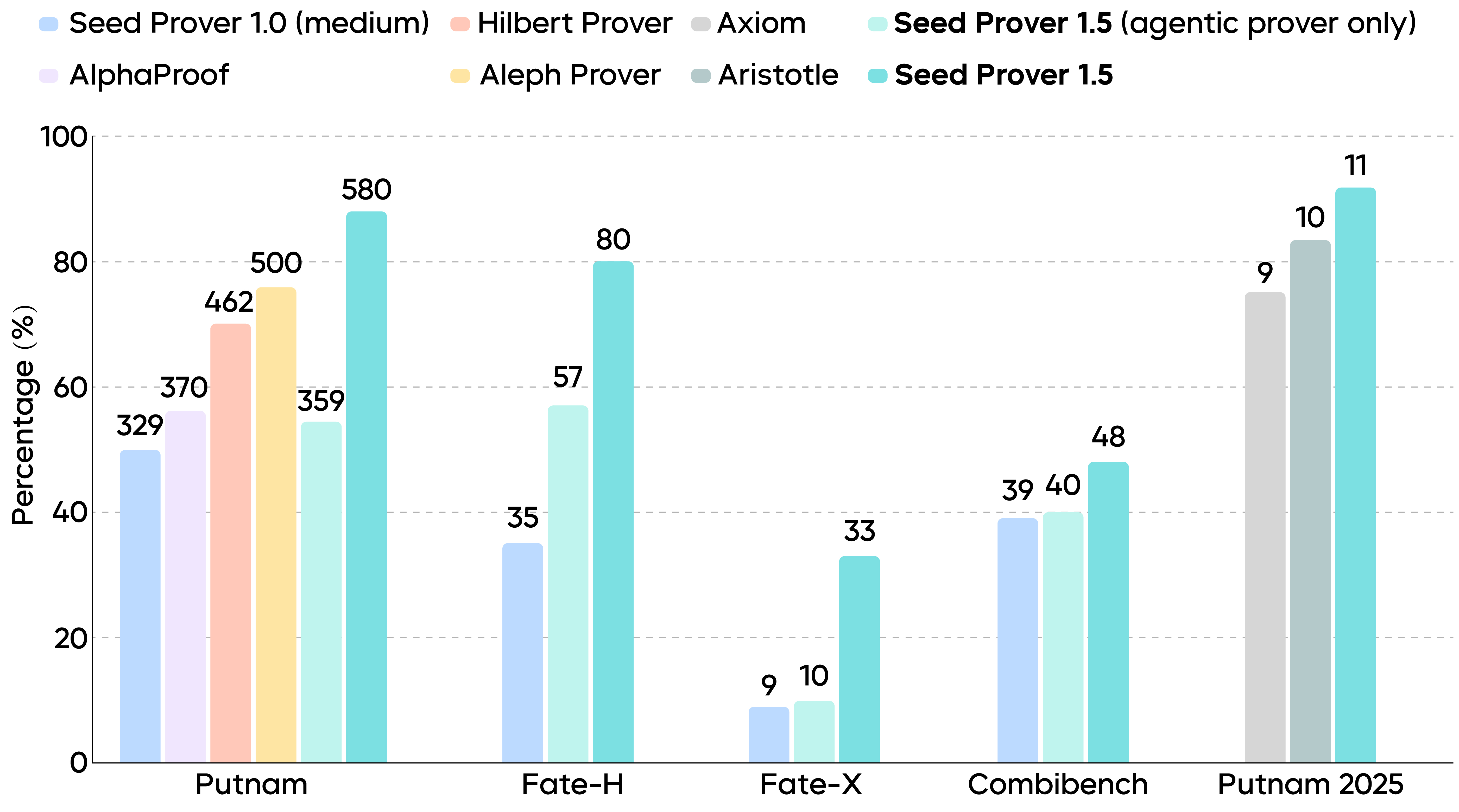
Performance comparison between Seed Prover 1.5 and previous SOTA methods across various benchmarks (numbers above the bars represent the total number of problems solved).
The technical report for Seed Prover 1.5 has been released. We plan to open API access in the future, inviting researchers in mathematics and AI to experiment with the model.
Tech Report:
https://arxiv.org/abs/2512.17260
Lean Proof Code
https://github.com/ByteDance-Seed/Seed-Prover/blob/main/SeedProver-1.5/Putnam2025.zip
1. Agentic Prover: A Novel Paradigm for Formal Mathematical Reasoning
Large language models (LLMs) can now fluently solve many mathematical problems using natural language. However, when confronted with highly complex cutting-edge mathematical research, natural language proofs often suffer from logical leaps or ambiguous definitions, making it difficult for mathematicians to fully trust them. In contrast, formal mathematical reasoning requires models to use formal languages such as Lean to construct proofs that can be mechanically verified within an axiomatic system. This gives formal proofs a significant advantage over natural language proofs in terms of ensuring correctness.
Yet precisely because of this, formal proofs are considerably more challenging than natural language proofs. According to the empirical "De Bruijn factor", a single line of ordinary mathematical derivation typically expands into 4 to 10 lines of complex code. This demands that the model be not only mathematically competent but also proficient in programming and type theory. Due to this high barrier, formal proofs have consistently lagged far behind natural language reasoning in both efficiency and success rates.
In previous research, formal provers have generally fallen into two categories: one is the meticulous but inefficient "step-prover", and the other is the "whole-prover", which attempts to generate a complete proof in a single pass but is highly prone to complete failure if any error occurs midway.
To bridge the gap with natural language reasoning, Seed Prover 1.5 introduces an innovative Agentic Prover architecture that balances the trade-offs between two formal proving methods. It treats Lean as a foundational tool and can autonomously invoke various auxiliary tools throughout the proving process.
-
Mathlib Search Tool: Similar to programmers consulting technical documentation, the model can actively search Lean's extensive mathematical library, Mathlib, to find applicable theorems and definitions, rather than relying on fallible implicit memory.
-
Incremental Lemma Verification: Instead of attempting to generate a full proof in one go, the model can now decompose complex problems into simpler, independent lemmas. Each proven lemma is stored and reused as a building block in subsequent reasoning steps.
This design allows the model to flexibly adjust its strategy: It can reason on a natural language "scratchpad" like a human, call on tools to verify mathematical conjectures at any time, and finally assemble the verified components into a complete formal proof.
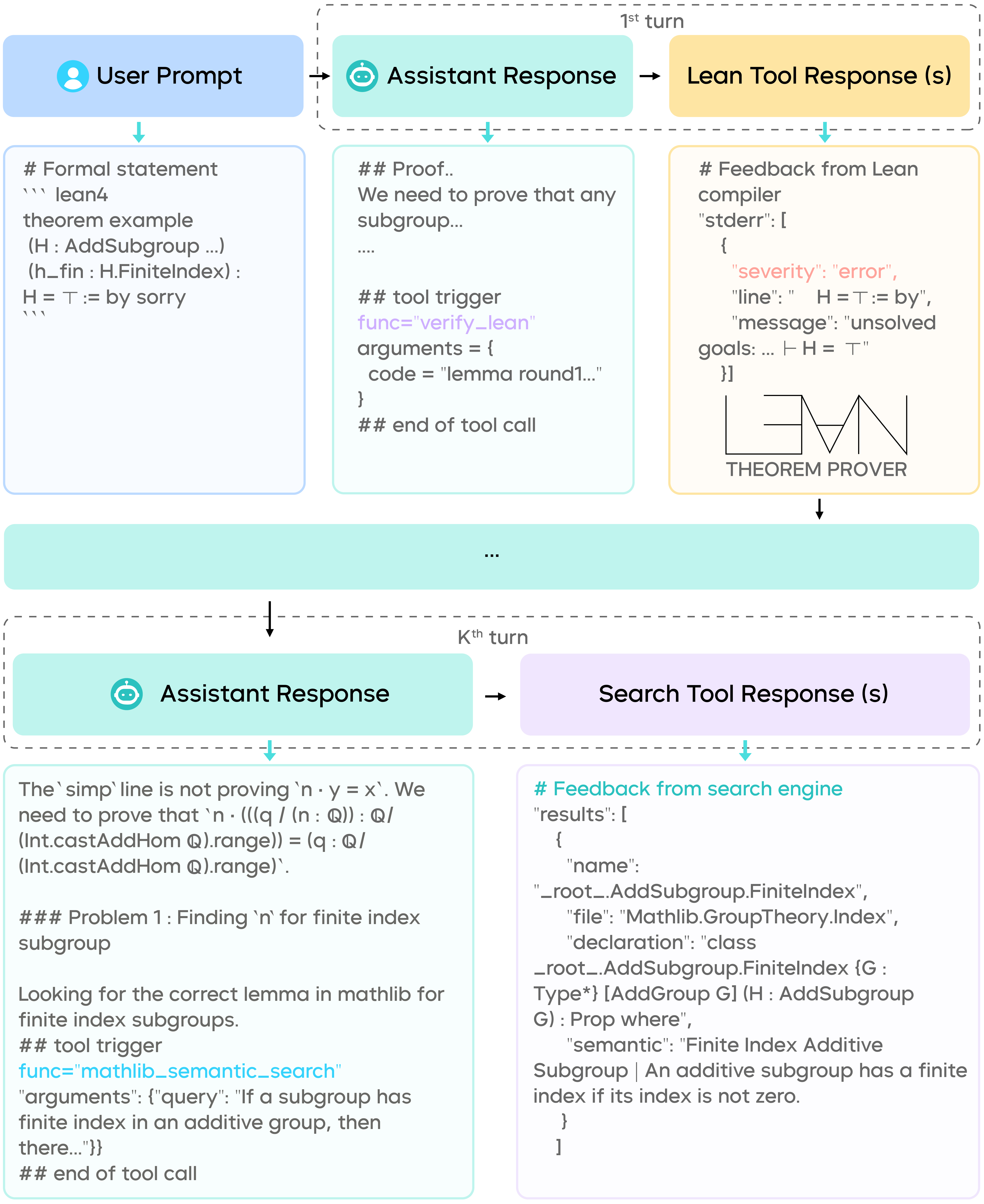
Example of Seed Prover 1.5 using tools to solve a FATE-H problem.
The robust performance of Seed Prover 1.5 is driven by large-scale Agentic RL. The model underwent extensive self-exploration and training within a purpose-built environment. Thanks to the Lean compiler's absolutely objective "correct/incorrect" feedback, high-quality reward signals were provided for reinforcement learning. Experiments show that as the number of RL training steps increased, the model's proof success rate on the training set rose from an initial 50% to nearly 90%.
Agentic RL also delivers a significant leap in efficiency. Comparative benchmarks reveal that Seed Prover 1.5 outperforms its predecessor on challenging datasets such as Putnam and Fate, despite requiring only minimal computational resources. This advance in both reasoning capability and efficiency represents a major step toward making formal verification practically viable.

Seed Prover 1.5 demonstrates a clear lead over Seed Prover 1.0 in both performance and efficiency (under the pass@8*8, computational cost is approximately 0.4 GPU days per problem).
2. Sketch Model: Bridging the Gap Between Natural and Formal Languages
While empowered by the Agentic Prover, generating complete formal code for complex theorem proofs—often spanning tens of thousands of lines—remains a formidable challenge. To address this, we trained a Sketch Model that mimics the problem-solving process of human mathematicians: establishing a high-level proof framework before delving into specific technical details.
This model can decompose a natural language proof into several independent, more manageable lemmas, temporarily skipping detailed proofs while preserving the overall logical structure. This approach clearly transforms otherwise intractable propositions into significantly easier sub-goals.
To train an excellent "proof architect", we employed a reinforcement learning strategy with hybrid reward signals:
-
Signal 1: The Lean compiler verifies the structural correctness of the generated proof sketch.
-
Signal 2: The Natural Language Prover checks each lemma individually. If any lemma is mathematically invalid, the entire sketch is rejected.
-
Signal 3: We introduced a Rubric scoring model based on Long Chain-of-Thought (Long-CoT) to assess the quality of the sketch at a semantic level—evaluating whether the lemmas align with the natural language proof, whether the decomposition granularity is appropriate, and whether it genuinely reduces the difficulty of the original problem.
Ultimately, the sketch receives positive rewards only when it meets all requirements in formal verification, mathematical correctness, and overall scoring.
Building on the Sketch Model, we also developed an efficient testing workflow, resulting in a hierarchical multi-agent collaboration system:
-
Natural Language Prover: Provides high-level mathematical intuition and natural language proofs.
-
Sketch Model: Converts natural language proofs into lemma-Style Lean sketches.
-
Agentic Prover: Executes formal proofs for each decomposed lemma in parallel.
If a lemma is too difficult to prove, the system recursively invokes the Sketch Model for further decomposition. This "divide-and-conquer" strategy mitigates error accumulation during long-text generation and fosters greater parallelism and higher success rates in reasoning.
3. Future Outlook: AI Advancing Toward Resolving Open Mathematical Problems
While current AI systems excel at solving well-defined, self-contained mathematical problems, such as those from the IMO or Putnam competitions, they still fall significantly short of making contributions comparable to human experts. This limitation stems from the "dependency issue" inherent in frontier mathematical research. Unlike competition problems, which can be tackled without deep familiarity with prior literature, driving significant progress in mathematics typically hinges on synthesizing insights across a multitude of related papers.
To evolve AI from a skilled "problem solver" into a genuine "researcher", we must address three interconnected challenges:
We will embark on an exploration of these major challenges in the coming years. It is hoped that in the near future, AI will be able to collaborate with human mathematicians to collectively tackle open mathematical conjectures.


